W/m^2, Altitude and the Hour Record. Part III

In my previous posts on this topic I explored the impact of altitude on the hour record. You can recap by clicking on the links here:

W/m^2, Altitude and the Hour Record. Part I
W/m^2, Altitude and the Hour Record. Part II

In summary, the primary impacts on the speed attainable (or distance attainable for an hour) are:

1. Physiological - the reduction in sustainable aerobic power as altitude increases due to the reduced partial pressure of Oxygen, and

2. Physical - the reduction in aerodynamic drag as altitude increases due to the reduction air density.

Of course there are other factors - variable track surfaces and geometry, logistical, financial, physiological and so on, but for the purpose of this exercise I have confined analysis to the primary physiological and physical impacts.

These primary competing factors - reduced power and reduced drag combine to mean that in general an increase in altitude means a greater speed is attainable. In other words, the benefit of the lower air resistance at higher altitude typically outweighs the reduction in power. But not always.

The level of impact to speed is individual and is a function of each individual's physiological response to altitude - while the physics side of the equation is the same for everybody. I covered this in more detail in Part II of this series, and used data from several studies which provide four formula for the average impact of altitude on power output.

I plotted the different formula depending on whether athletes had acclimatised to altitude or not.

This chart should be fairly intuitive - further up in altitude you go, the more power you lose compared with sea level performance. The vertical scale of the chart amplifies the differences between them, which are not large, but also not insignificant either. A key element was the difference between athletes that had acclimated to altitude and those who had not.

Then I layered on that the physics impact of reducing air resistance, but the resulting chart was not quite as intuitive to follow and so I decided to revisit this another way.

Hence exhibit A below (click on the image to view larger version):

This should be reasonably straightforward to interpret, but even so I'll  provide some explanation.

The horizontal axis is altitude and the dark vertical lines represent the altitude of various tracks around the world.

The vertical axis is the proportion of sea level speed attainable.

The curved coloured lines represent the combined impact of both a reduction in power using each of the formula discussed in Part II of this series, combined with the reduction in air resistance.

So for example, if we look at the green line (Basset et al acclimated), this shows that as an cyclist increases altitude, they are capable of attaining a higher speed up until around 2,900 metres, and any further increase in altitude shows a decline in the speed attainable, as the power losses begin to outweigh the reduction in air density.

The track in Aigle Switerland represents around a 1% speed gain over London, while riding at Aguascalientes would provide for between a 2.5% to 4% gain in speed. Head to Mexico City and you might gain a little more, but as the chart shows, the curves begin to flatten out, and so the risk v reward balance tips more towards the riskier end of the spectrum.

Altitude therefore represents a case of good gains but diminishing returns as the air gets rarer. Once you head above 2,000 metres, the speed gains begin to taper off, and eventually they start to reduce, meaning there is a "sweet spot" altitude.

Caveats, and there are a few but the most important are:
-  any individual's sweet spot altitude will depend on their individual response to altitude - the plotted lines represent averages for the athletic groups studied;
- the formula used have a limited domain of validity, while the plotted lines extend beyond that, a point I also covered in Part II of this series;
- these are not the only performance factors to consider, but are two of the most important.

I suspect that the drop off in performance with altitude might occur a little more sharply for many than is suggested here. Nevertheless, the same principles apply even if your personal response to altitude is on the lower end of the range, and it is hard to imagine why anyone would suggest that heading to at least a moderate altitude track is a bad idea from a performance perspective.

Alex Dowsett rode 52.937km at Manchester earlier this year. At Aguascalientes he could reasonably expect to gain ~3.5% +/-0.5%  more speed, or just about precisely what Bradley Wiggins attained in London.

Read More......

Wiggo's Hour

Just a short one today to update the chart from the one I posted here and on other social media forums. Click to see bigger version.

54.526km

Different reports of barometric pressure of 1031-1036hPa and air temp of 30.3C inside the track mean that Wiggins must have been exceptionally aerodynamic and recent work on his bike and position at the track suggest some good aero gains were made.

I estimate a power to CdA ratio of 2500-2550W/m^2 was required.

There are of course a range of assumptions:
Total mass: 82kg
Crr: 0.0023
Drivetrain efficiency: 98%
Altitude: 50m
Relative Humidity: 60%

If drivetrain efficiency is better, say 99% and Crr at 0.0020, then it drops the power to CdA ratio down to 2200-2220W/m^2.

and perfect pacing.

Just on that, my colleague Xavier Disley has once again produced a lap pacing chart - here it is:

That's a very slight fade over the course of an hour, which in my humble opinion is pretty much perfect. Opening few laps a bit hard, but that's understandable as a rider seeks to control the adrenaline rush with thousands in the crowd watching on and cheering.

The high air pressure did cost distance, and on another day perhaps 55km was within reach

As for going to high altitude, well there are many variables, but another 1-2km is feasible. See this item for more on that.

Well done to Brad Wiggins. That's sure a fine ride.

Read More......

Pressure on the Hour

My colleague Xavier Disley did up a neat chart showing the impact the daily variability of barometric pressure can have on the distance attainable for an hour record, and how it's looking given the weather forecast when Xav last did the chart:

Nice - it shows how much breaking a record can still come down to a bit of luck with weather.

I think in Wiggins' case, assuming no major execution (i.e. totally crummy pacing) or mechanical issues, he'll break Dowsett's current mark no matter the weather as his power to drag ratio is sufficiently higher than Dowsett to overcome a slow air day.

But to set an outstanding mark such as Rominger's record, he'll need luck on his side. High pressure days are not good for speed.

Below is another version of this relationship between barometric pressure and distance attainable for four combinations of power and aerodynamic drag (CdA) values.

The chart is pretty self explanatory. For each combination of power and CdA chosen, the distance attainable reduces as barometric pressure increases.

That's because higher air pressure means a higher density of air molecules, and more air molecules to push out of the way requires more power.

A 60hPa difference in barometric pressure is equivalent to about 1km difference in distance attainable for the hour for the same power and CdA. That's a wide range of barometric pressure though, and variations are not normally quite that wide in most locations.

But a variation of half that is certainly possible over just a few days of varying weather as can be seen in Xavier's chart above.

I chose two power outputs: 430W and 450W, and two CdA values: 0.20m^2 and 0.19m^2. I don't know what Wiggins' power nor CdA value actually is or will be on the day, but for the sort of speeds he's likely to attain, these are in the ballpark.

It's the ratio of power (W) to aero drag coefficient CdA (m^2) that primarily determines the speed or distance attainable. hence why we refer to power/CdA ratio as measured by W/m^2. This chart covers a power to drag ratio range of 2150-2370 W/m^2.

Read More......

Some kilometres are longer than others

With the spate of attempts at the UCI world hour record over late-2014 and into 2015 due to the revised UCI rules making the record within reach of more riders, it has naturally sparked interest in discussing what matters for best performance in the event.

Jens Voigt started the latest round of hour record attempts at the UCI's Aigle track

I recently saw some chat on a triathlon forum speculating about who could do what distance and so on. All in good fun, but none of them actually go to a track to find out. If they did, they'd realise it's not quite as simple (or as hard) as they might make out.

It pretty much comes down to optimising four main elements:

• maximising sustainable power output for an hour
• minimising the physical resistance factors of riding on the track
• technical execution / skill
• logistics & resources

Some might add psychological factors to that list, but ultimately I consider these to be expressed within the outcomes of each of the above.

Regarding logistics, there are of course UCI requirements to be permitted an official attempt an hour record, e.g.: minimum time in anti-doping bio-passport program is mandatory at elite level or dope testing at age group level, application submitted in advance for approval to relevant levels of cycling administrations, all the technical requirements including international level commissaires to supervise, a UCI approved track, use of timing equipment, start gates, specified date and time of attempt, etc. You can't just rock up and ride whenever you like. Well you could but it would never be a sanctioned attempt.

Then of course you need to factor in enough solo rider time on track for preparation, and that costs money and time as well. Quality indoor tracks are not always local, and even if they are, getting solo time on the track is not always so easy, let alone cheap. For an elite professional rider whose job is to race on the road, it may be difficult to devote sufficient time to the task of preparing properly for a track event.

Of course assuming the paperwork is all in order and you can do your training, then sustainable aerobic power and aerodynamics are king and the rider's ratio of power to aerodynamic drag area is the single most important factor for how far they will go in the hour. But W/m^2 is not the only factor.

There are other physical resistance force factors, like the influence of air density which is a function of altitude, temperature and barometric pressure (and to a much lesser extent, humidity) and the rolling resistance of the track and tyres chosen. I discuss some of these in the following items:
Altitude and the Hour record Part I
Altitude and the Hour record Part II

Which leaves us with technical execution and skill factors, of which there are a couple of key items, namely:

• pacing, which I covered in this case study of the masters hour record by Jayson Austin, and 
• riding a good lines around the track.

Riding good lines

Riding a good line involves a couple of components, one is pretty obvious and involves not riding further than you need to around the bends. Ride wide and you ride further. Pretty simple given the track is all but two semi-circles joined together with two straight sections. OK, the actual shape of tracks are more subtlety curved but that's close enough to describe why riding wide adds distance to your travels around a lap.

Design of the Glasgow Velodrome

If you ride 10cm wider in the turns, you add 10cm x 2 x PI = 62.8cm per lap.

If the extra width is measured on the track's surface, well the actual addition to the distance the wheel travels is reduced by the cosine of the banking angle. e.g. say the track's turns are, on average, banked at 40 degrees, and you ride 10cm above the black line. Then the actual additional track radius ridden is cosine (40 degrees) x 10cm = 7.7cm, and the additional distance per lap = 7.7cm x 2 x PI = 48.1cm. Nearly half a metre.

Do that over 200 laps or so for an elite hour record and you'll ride ~100 metres more than you need to. And that's for riding only a hand's width above the black line.

London Velodrome used for the 2012 Olympics

Another more subtle ride line factor involves the shape and design of the banking and in particular the transitions from the straights to the turns and back again, and whether it's advantageous to ride a slightly wider line in the straights to aid the transitions. On the straights you don't suffer the same severe distance penalty of riding a wider "radius" as you do when riding wide in the turns, so you can explore marginal gains in this manner.

However there is no simple or single answer to this, it depends on the rider and the track geometry - all of which have subtle differences. This is a somewhat more complex optimisation problem and I'm not going to delve into it here.

So putting aside these subtleties, the shortest distance around the turns is to ride the track's black measurement line* - ride any further out from the black line and you ride more distance each lap than is necessary. For the hour record you only get credit for the official lap distance each lap, which is typically 250 metres per lap on most modern standard indoor velodromes although some tracks are shorter and some are longer.

* it is possible to ride inside the black line, however in such timed track events like the hour there are foam blocks placed around the inside line of the track to ensure the riders don't. Very skilled riders can however ride fractionally under the black line on some tracks but it is risky as hitting the foam blocks can disrupt your effort and wash off some speed. The shape of the track in that small space between the black line and the wide blue section varies from track to track and it can be good or not so good to ride in.

Foam blocks discourage riders from riding inside the black measurement line.

Now why are some kilometres longer than others?

Office distance for the hour record =
(Official lap distance)  x  (Number of full laps completed within the hour)
+ a pro-rata distance calculated for the final incomplete lap

I won't go into the formula used by the UCI to calculate the pro-rata distance of the final lap (that's actually deserving of a blog post on its own as the regulations are remarkably confusing).

It matters not how far you actually ride, you'll only be credited with the official minimum lap distance per lap. This is why track riders and coaches are focussed on lap times and not with bike speed, since lap times are the integral of all performance elements. Power meter and other data loggers are of course valuable in parsing out the individual elements of performance that go into attaining lap times, and helping to prioritise development opportunities.

How good are riders at riding the minimum distance necessary?

It varies. Quite a lot. Skilled track riders are typically much better, which is what you'd expect. But what sort of penalty would an unskilled rider face if they started out on a track effort?

Of course we can do lots of maths to figure out how much extra distance on average a rider might cover if they ride wide by so much, but in reality riders move up and down the track, sometimes riding a good line, other times not so good. Some riders are just better at it than others and some adapt to the track more quickly than others.

It'd be so much better if we could simply measure what people actually do rather than speculate.

Which had me thinking. I have some data like that already...

Not so long ago I was doing some performance testing involving half a dozen pro-continental road racers at an indoor 250m velodrome. One of the features of the data logging system used for the tests is an ability to calculate the distance ridden per lap using the wheel's speed sensor data combined with track timing tapes to know precisely when they pass a specific points on the track. With some clever maths this is enough to nail the actual distance ridden each lap to high precision.

In amongst the test data were some solo efforts of at least 10% of the distance of an elite hour record attempt (i.e. 20+ laps of consistent effort) and several such runs by each of the six riders. I figured the runs needed to be long enough to reasonably approximate what a rider might be expected to do over a longer distance/duration.

Of course absolute accuracy of the distance the wheels travel depends on having an accurate wheel circumference value and that value not changing a lot while riding. So I'm not going to assume that the absolute accuracy was perfect, even though the absolute error might typically be somewhat less than 1%. More than that would require an error in tyre circumference assumption of 20mm, which is a lot for those used to measuring such things. However in our favour is that even if such an error existed, it would be a consistent bias error.

So rather than concern myself with absolute accuracy, I thought I'd compare the measured average lap distance for each run with the shortest recorded legitimate lap. In this way if there is any bias error, it's impact on this analysis is minimised (i.e. both measurements would be out by the same proportional amount). By legitimate lap, I mean a full lap not ridden below the black line.

Here's a table summarising data collected from the six riders (in no particular order). Each rider has multiple runs although I haven't identified the riders in the table. What the first column shows is the average lap distance per run less the minimum legitimate lap distance for that same run. The distances are of course distance travelled by the wheel.

Now the riders possibly could ride a tighter line than they actually did for their shortest legitimate lap, meaning that these distances likely underestimate the extra distance ridden when compared with riding very tight to the black line.

For the moment though let's assume the shortest lap they rode during each run was the best they are capable of doing. Since they actually did it, I think that's a reasonable assumption.

The average extra distance ridden per lap varies from one rider to another. One rider consistently rode only 0.3-0.4 metres more per lap than their shortest distance lap, while another was consistently riding more than 2 metres extra per lap on average compared with their shortest legitimate lap. The rider with smallest extra distance per lap had a track racing background.

The second column shows what that average extra lap distance would mean if extrapolated to riding 200 laps of a 250m track (an official distance of 50.000km). For one rider they would be riding nearly half a kilometre further than their track skilled team mate. Yet if both completed exactly 200 laps in the hour, each would be credited with riding precisely 50km, even though one rider's wheels had travelled nearly 500m further than the other's.

In this case, 50.5km = 50.0km. Some kilometres are longer than others.

So what's that extra 500m cost in power terms?

Well for a rider with a CdA of ~0.23m^2, that extra 500 metres travelled requires they output ~11-12 watts more than if they were able to ride a a better line.

Or they'd need to find a 3% reduction in CdA to make up for their skill deficiency.

Remember these were well skilled, well trained and experienced pro-continential road racers and finding an extra 10W or losing another 3% of aero drag coefficient isn't such an easy thing to do.

So no matter your current skill level and experience, if you're expecting to ride such an event yet you have never trained to become proficient riding on the track, well you might want to chop half a kilometre or so from your estimated distance covered based on your power and aero data alone.

Better still, just get to a track a find out what you can actually do.

Likewise, when estimating power, or W/m^2 from the official hour record distances, you might need to add some watts for the technical proficiency of the rider. The less proficient, the more power is required to attain the same official distance.

Read More......

W/m^2, Altitude and the Hour Record. Part II

The Physics recap

In an earlier blog post I examined the influence of altitude on the physics of cycling’s world hour record, and showed how the reduction in air density as altitude increases means one can travel faster for the same power output, or put another way, the power demand reduces at any given speed as altitude increases.

That resulted in this chart, which shows the relationship in power to drag ratio (W/m^2) for speeds ranging from 47km/h up to Chris Boardman's 56.375km/h record. I've slightly amended the chart to extend up to altitude of 3,000 metres. Click on the pic to see a larger version.

Each slightly curved coloured line represents a speed as marked, and from that you can see how the W/m^2 required reduces with increasing attitude. The chart clearly suggests there is an advantage to performing such record attempts at higher altitudes, but it's never that simple of course. 

And the Physiological impact...

As we climb to higher altitudes and air density drops, the "thinner" air also means a reduction in the partial pressure of oxygen, which negatively impacts the power output we can sustain via aerobic metabolism. That loss of power can be as much as 20% or more depending on how high we go, and our individual response to altitude.

So the gain in speed from the physics side of the equation is somewhat negated by the reduction in physiological capacity. But by how much, and what might be the optimal or "sweet spot" altitude for a cyclist seeking to set a new record?

The physics side of the equation is easier to predict than the physiological, since the physics applies equally to all, however individual physiological response to altitude is quite variable, both from person to person, but also depending on how well a rider has acclimated to altitude. There are even differences in how altitude affects elite versus non-elite riders.

There have been a few published papers examining the impact of altitude on aerobic athletic performance and from these formulas to estimate the loss of power as a function of altitude have been developed. There was one from the 1989 paper by Peronnet et al, two from the 1999 paper by Bassett et al, one each for acclimated and non-acclimated athletes. Adding to those, I have generated a fourth formula, based on the 2007 study by Clark et al. The relevant papers are:

Péronnet F, Bouissou P, Perrault H, Ricci J.:
A comparison of cyclists' time records according to altitude and materials used.

Bassett DR Jr, Kyle CR, Passfield L, Broker JP, Burke ER.:
Comparing cycling world hour records, 1967-1996: modelling with empirical data.

Clark SA, Bourdon PC, Schmidt W, Singh B, Cable G, Onus KJ, Woolford SM, Stanef T, Gore CJ, Aughey RJ.:
The effect of acute simulated moderate altitude on power, performance and pacing strategies in well-trained cyclists.

Peronnet et al used empirical data from actual world cycling hour records to estimate the impact of altitude on an elite cyclist's power output. The assumptions used in estimating altitude induced power loss may have some error; in particular due to methods used to estimate the power for each rider as neither the power nor coefficient of aerodynamic drag was actually measured.

According to the old Wattage forum FAQ item by Dr David Bassett, Jr, the two Bassett et al formula were derived from earlier papers examining altitude impact on aerobic performance of four groups of highly trained or elite runners. So while these formulas were not derived from cyclists we can still generalise from those to the loss of aerobic capacity for cyclists.

Finally, the study by Clark et al measured the impact on peak oxygen utilisation (VO2), gross efficiency and cycling power output on ten well trained but non-altitude acclimated cyclists and triathletes by testing riders at simulated altitudes of 200, 1200, 2200 and 3200 metres. They examined a number of factors, including maximal 5-minute power output, VO2 and gross efficiency relative to performance at 200 metres, as well as sub-maximal VO2 and gross efficiency.

I used these data to generate a formula similar to those from Peronnet et al and Bassett et al. Of course there is an assumption of an equivalent reduction in 1-hour power as for 5-minute power. Clark et al noted slightly greater reductions in VO2 peak than for 5-minute maximal power, and no change in gross efficiency at 5-min max power with altitude. So there is some anaerobic metabolic contribution presumably making up the difference. There was some loss of sub-maximal efficiency noted at a simulated 3200 metres.

I chose in this instance to use the reduction in 5-minute power rather than fall in VO2 peak as the base data for the formula, and applied an adjustment to offset the formula for sea-level equivalency to bring it into line with the formula by Peronnet et al and Bassett et al. Of course when you look at the reported data there are of course sizeable variations within the test group at each simulated altitude, so the formula is based on group averages for each simulated altitude.

Here are the formulas:

x = kilometres above sea level:

Peronnet et al:           
Proportion of sea level power = -0.003x³ + 0.0081x² - 0.0381x + 1

Bassett et al Altitude-acclimatised athletes (several weeks at altitude):
Proportion of sea level power = -0.0112 x² – 0.0190x + 1
R² = 0.973

Bassett et al Non altitude-acclimatised athletes (1-7 days at altitude):
Proportion of sea level power  = 0.00178x³ – 0.0143x² – 0.0407x + 1
R² = 0.974

Simmons’ formula based on Clark et al:
Proportion of sea level power  = -0.0092x² – 0.0323x + 1
R² = 0.993

So how do each of these estimates of power reduction at altitude compare? Well here's a plot of these formula:

There is some variance between each formula's estimates, although the gap between the Non-acclimatised athlete estimates by Bassett et al and by Simmons based on Clarke et al is not all that large, ranging up to a ~2% variance. 

Had I chosen to use the reduction in peak VO2 for 5-min max power, then I'd expect those two lines to be closer. In any case, these data by Clark et al reasonably match earlier reported findings of the impact of altitude on sustainable aerobic power. And once again - the individual response varies - these are simply averages based on the limited data available and for the cohorts tested. As always, YMMV.

The formula by Peronnet et al is the least aggressive at reducing the estimate of a cyclist’s power at higher altitudes, and that may be due to various not insignificant assumptions used in calculating each rider’s power outputs.

OK, so now we have estimates of both the physics upside and the physiological downside of altitude, What happens when we merge the two?

Well if I recreate the chart showing the physics, and overlay on that the curve showing power output as a function of altitude, this is what we get if we examine a rider capable of sustaining 51km/h at sea level:

Let me explain how to interpret the chart.

First of all, the vertical axis scale has been changed for clarity – the slightly curved coloured lines still represent the power to drag ratio required to attain a given speed at various altitudes.

So let's examine the case for a rider capable of sustaining 51km/h at sea level.

The thick orange line represents the power to drag required to sustain 51km/h. At sea level that's ~1,800 W/m^2 (Red circle 1). The exact value depends on a few other assumptions of course, so let's just use that as our "baseline" W/m^2 value.

Now if we apply the Bassett et al formula for power reduction for an altitude-acclimatised athlete, then their baseline sea level power (and with it their power to aero drag ratio) falls with increasing altitude. This drop in sustainable power with increasing altitude is indicated by the black dotted line.

We can see the power to drag ratio resulting from the physiological impact of altitude (the dotted black line) doesn't fall as quickly as the power to drag ratio required to sustain 51km/h (the thick orange line).

If you trace the black dotted line from left to right, we can see that at Red Circle 2, the power to drag ratio crosses the line marked 52km/h at an altitude of ~700 metres. Then as you trace the dotted line further to the right, we can see it cross the 53km/h line at ~1,500 metres. Tracing the line to the right hand edge of the chart out to 3,000 metres altitude, we can see it doesn't quite reach the 54km/h line, falling a little short at 53.9km/h. So for this altitude-acclimatised athlete, they can gain an extra 2km on their hour record simply by choosing to ride at an altitude of 1,500 metres.

OK, so what happens if the athlete is not acclimatised to altitude?

This time the non altitude-acclimatised power line is indicated by the lower black dashed line. It starts at 1,800 W/m^2 at sea level indicated at Blue circle 1, but as we trace that line to the right, it falls away more quickly than for the altitude-acclimatised athlete, crossing the 52km/h line at ~1,000 metres altitude (Blue circle 2) and not reaching the 53km/h line by the time the athlete is at 3,000 metres, where in this case the athlete would be estimated to achieve a speed of ~ 52.9km/h (Blue circle 3).

So while the acclimated athlete can improve their speed by 1km/h by going from sea level to 700 metres, and increase speed by 2km/h by going up to 1,500 metres, to achieve the same speed gains the non-acclimated athlete would need to ride at an altitude of 1,000 metres and would not be able to attain a 2km/h speed gain even at 3,000 metres.

We can see that as the altitude increases, the extra speed gains begin to diminish, and there are risks in going too high, especially if you are not acclimated, or experience an above average decline in power with altitude.

Conversely, if you are well acclimated and/or have a below average decline in power with altitude, then there are benefits in going higher if maximising speed is your primary objective.

Any rider considering an hour record would do well to consider the opportunity presented by tracks located at altitude. Of course costs, logistics, regulations all factor into the choice of venue, and how much time a rider may need to acclimate to altitude, and their individual response to altitude.

If a sea level based rider were considering a fly-in / fly-out attempt without much acclimation time, then I'd suggest choosing a good track that is not too high, as the risks of a larger than expected power decline increase significantly, and the potential speed gains diminish as well increasing complexity of execution as nailing pacing gets trickier. Of course the more experience a rider has with altitude and its impact on their performance, the more confident they can be with predicting an ideal location.

So what tracks are there at altitude?

Indoor laminated wooden 250m tracks at altitude include:

• Aguascalientes, Mexico: 1,887 metres above sea level
• Guadalajara, Mexico: 1,550 metres above sea level
• Aigle, Switzerland: 415 metres above sea level
• Astana, Kazakstan: 349 metres above sea level
• Grenchen, Switzerland: 340 metres above sea level

There are track at much higher altitudes, but they are 333 metre outdoor tracks with concrete surfaces:

• La Paz, Bolivia: 3,340m
• Cochabamba, Bolivia: 2,571m
• Arequipa, Peri: 2,295m
• Mexico City, Mexico: 2,260m

Of the above listed tracks, Aguascalientes is a venue well worth considering. Eddy Merckx's October 1972 hour record of course was set in Mexico City, as were Francesco Moser's two hour records in January 1984. Most hour records since then have been set at or near sea level, with the recent rejigged rule records set by Jen's Voigt and Matthias Brändle at the Aigle and Grenchen tracks in Switzerland respectively.

So what's actually possible by the bigger guns of the sport. e.g. Wiggins, Martin, Bobridge and company?

I'll save that analysis for a future post, as well as a look at generating a formula to estimate the range of potential speed gains as a function of altitude, given an estimated sea level performance.

Read More......

W/m^2, Altitude and the Hour Record

More hour record stuff to follow on from the item on Jens Voigt's hour ride.

This time to look at the physics impact of increasing altitude. I'll layer on top of this the physiological impact in a future post.

tldr version, click on this chart:

In brief:
- for a given W/m^2, you'll go faster as altitude increases
- for a given speed, the W/m^2 required reduces with altitude
- for a given altitude, to go faster the W/m^2 required increases

Now the long version:

There are two major factors which determine the speed a rider can maintain on flat terrain such as a velodrome, that being their power output and the air resistance. Or put another way, these are the primary energy supply and demand factors. There are other smaller energy factors as well (mostly on the demand side) but power output and air resistance are by far the most important when it comes to riding an hour record attempt on velodromes (or any race of individual speed on flatter terrain).

Energy Supply

What power output one can sustain for an hour is a function of several underlying factors that I discuss in this post. We influence that primarily through training, and of course to a large extent it depends upon the genetic gifts we are blessed with*.

There is of course also the physiological impact of altitude, as the partial pressure of oxygen reduces with increasing altitude, and as a result, so reduces the power we are able to maximally sustain aerobically (with oxygen). How much reduction in power occurs with altitude is individually variable, and you can acclimate to some extent as well, but there is no denying that once altitude starts getting high, ability to generate power definitely falls away.

I go through some of this in this post on altitude training, and I will be returning to this and its impact on hour records in a future post.

Energy Demand

For hour records on a velodrome, air resistance accounts for more than 90% of the total energy demand factors. In the case of  indoor velodromes and speeds in the 50-56km/h range, it's of the order of 92-93% of the total energy demand, with the balance mostly being rolling resistance and other frictional energy losses, and a tiny fraction in kinetic energy changes. This dominance of air resistance in the energy demand is why there is such a solid relationship between speed and the ratio of power to aerodynamic drag.

Air resistance & CdA

Air resistance on a cyclist is a function of several factors, being:
- the bike and rider's coefficient of air drag (Cd),
- their effective frontal area (A),
- the speed they are travelling at,
- the speed and relative direction of any wind, and
- the density of the air.

The coefficient of drag (Cd) and frontal area (A) multiply together to give us a measure of a rider's air resistance property - CdA. A lower CdA means you can go faster for the same power, or less power is required to sustain the same speed.

CdA is something a rider can change through bike positional and equipment choices (e.g. using an aerodynamic tuck position reduces your CdA compared with sitting more upright, or using deep section wheels with fewer spokes lowers CdA compared with using shallow box section rims with lots of spokes).

So to ride faster on an indoor velodrome where there is no tail or head wind to aid or hinder, you'll need to either:

- increase your power output, or
- reduce your CdA, or
- reduce the density of air you are riding through.

Or of course some net combination of all three that results in more speed.

It is possible that one can produce less power but have a significant reduction in air resistance factors such that the resulting speed is higher. For example, sometimes there is trade off between the advantage gained from use of an aerodynamic position on a bike, even though there may be a sacrifice of some power output due to the impact the aggressive bike position has on a rider's bio-mechanical effectiveness.

It all boils down to W/m^2

Robert Chung some years ago published a nice chart that shows the equivalency of speed on flat terrain with the ratio of power to CdA:

What we can see in this chart is how well Power/CdA can help estimate speed on flat road terrain over a wide range of power outputs and CdA values. Of course it's not a perfect correlation, as you can attain a slightly higher speed with the same W/m^2 as the power (and CdA) increases. So even if you share the same W/m^2 as another rider, the rider that has more absolute power will still be ever so slightly faster.

Not by much though. As an example, if we compared two riders on a low rolling resistance velodrome, one with 400W and another with 10% more power (440W) and both had the same power to CdA ratio of 1700W/m^2, then the more powerful rider will only be ~0.1km/h or 0.2% faster (all else equal). Like I said, there's not much in it.

I also showed this in the chart from my previous post on the Jens Voigt hour ride, where estimating his W/m^2 with reasonable precision is much easier than his absolute power. If the power was lower, so the W/m^2 must be a little higher, but not by much. Over a 100W (25-30%) range of possible power outputs, the W/m^2 required to attain the same speed varies by only 2%.

So even if we consider a range of power outputs typical for elite riders of the calibre likely to attempt an hour record ride, the W/m^2 ratio required for a given speed on a given velodrome will be within a pretty tight range.

Air density

Air density however isn't quite as easy for an individual to control, as it is largely a function of environmental conditions, in particular:
- air temperature,
- barometric pressure, and
- altitude.

Air density drops with an increase in temperature and altitude, and with a reduction in barometric pressure. Humidity also affects air density, but only by a very small amount (humid air is marginally less dense than dry air). So while a rider cannot control the atmospheric barometric pressure, they can choose a velodrome with a temperature control system, or one that will likely be warm, as well as choose from a range of tracks that are at different altitudes.

Altitude and its impact on speed

So given all that, I thought I'd look at how the combined effect of the power and aero drag values required to ride at certain speeds varies with altitude. As is typical of me, I've summarised this in a chart shown below. As usual, click on the image to see a larger version.

It's not overly complex, but let me explain.

On the vertical axis is the ratio of power output to the coefficient of aero drag x frontal area (CdA). Power / CdA in units of watts per metres squared.

On the horizontal axis is altitude in metres.

Then I have plotted a series of slightly curves lines, one each for speed ranging in 1km/h increments from 47km/h to 56km/h, and another line for 56.375km/h, which is the speed Chris Boardman averaged for his hour record.

For the sake of comparison, I've fixed the air temperature, barometric pressure, bike + rider mass and rolling resistance to be constant values for each. I did a little variation of power, but not much, and as I have demonstrated, the impact is very small.

So if we look at any particular line, we can see how the W/m^2 required to sustain that speed reduces as altitude increases. And of course we can see that for any given W/m^2 the speed you can sustain varies with altitude.

e.g. let's take 1800W/m^2. At sea level, the 1800W/m^2 line crosses the 51km/h line. As you trace horizontally from left to right, the 1800W/m^2 crosses the speed lines roughly as follows:
51km/h @ sea level
52km/h @ ~500m altitude
53km/h @ ~1000m
54km/h @ ~1450m

55km/h @ ~1950m

56km/h @ ~2450m

So naturally there is interest in using tracks at higher altitudes in order to ride faster and set records.

Now of course different tracks have variable quality surfaces, and so the assumption of rolling resistance being equal at all tracks is not valid, so any comparison of actual tracks should also consider impact of changes to coefficient of rolling resistance (Crr). Even so, since Crr accounts for only ~ 5-6% of the total energy demand, then track smoothness, while a factor, is more important when considering tracks at similar altitudes.

But what about power output at altitude?

Well of course there is a trade off between the speed benefit of lower air density at increasing altitudes, and the reduction in a rider's power output as partial pressure of O2 falls.

Hence as altitude increases, while a rider's CdA will not change, their power output will fall and hence their W/m^2 will also fall accordingly. So the W/m^2 line for any individual won't be horizontal, but rather trend downwards from left to right.

How quickly an individual's W/m^2 line drops away with altitude then determines the real speed impact of altitude.

So, what's the optimal altitude for an hour record?

I'm going to explore that in a future post (although I'm certainly not the first to have done so). So stay tuned.


* Pithy Power Proverb: "Choose your parents wisely".

Read More......

Hour record: Jens Voigt

Plenty has been written about Jen's Voigt's successful attempt at the new UCI hour record, set under the recently revised rules which permits the same bike set up currently used for the individual pursuit.

I thought I'd just add a chart to illustrate what sort of power and aerodynamic drag would be required to attain the result Jens achieved. The chart below summarises these key numbers and plots the CdA v power required, and shows the ratios of power to coefficient of drag area and power to body mass.

Where on that line Jens was, I don't know exactly, but it will be somewhere along there, or nearby. Click on the chart to open a larger version so you can see the numbers.

Jens' power to CdA ratio was in the range of
1715 - 1750 W/m^2.

Let me add some detail as to how the chart is derived, the assumptions used and key sensitivities. First the numbers we know.

Distance travelled and speed
Jen's official distance for the hour was 51.115km, which is calculated by the number of whole and partial laps completed x 250m per lap. Now we know from video that Jens did not always ride a perfect line around the track, and so his wheels actually travelled further than the official distance. Riding a good line is all part of the skill of track racing, so Jens likely cost himself some official distance.

So when calculating what speed Jens was actually doing, we'd need to know his actual wheel speed or distance per lap. However since air resistance acts mostly on where the centre of mass of the bike and rider is, which on a velodrome travels a distance less than that of the wheels, then we'd also need to factor in the lean angle of the bike and rider. Now I'm not going to attempt to do that. The data does actually exist as it was recorded by the Alphamantis Track Aero System which performs such calculations on the fly, but I don't have it.

In any case, I am going to assume that the extra distance travelled by Jens' wheels was cancelled out by the lean angle meaning Jens' centre of mass travelled about the same as the officially recorded distance. It's difficult without more data to be more precise than that, but it's a reasonable assumption.

Complicating the speed equation was Jens' pacing, which was somewhat variable, starting strongly, falling into a lull and then increasing somewhat in the final 10-15 minutes of the ride. So there would have been quite some variations in the power output during the ride. Of course the event starts from a an electronic gate that holds the rider, and there is some extra effort require to get up to speed which takes 10-15 seconds, so while it's a factor, it's a pretty small one in the the overall hour.

Here is a picture posted by Xavier Disley on his twitter account, showing lap by lap speeds, and when Jens got up out of saddle briefly:

In any case, I am going to work with the overall average speed of the rider as 51.115km/h.

Environmental conditions
Based on Weather Underground link the following conditions existed at the time of the ride:

Air pressure: 1012hPa
Humidity: 60%
Outdoors there was a light wind of 2-3km/h and no precipitation.

Temperature:
A spectator at the track reported the temperature indoors was 26C. Outside it was 20C with a maximum of 23C, so the reported indoor temperature is plausible and I'll go with that.

Altitude:
430m at Grenchen, Switzerland.

All of this provides an air density value of 1.114kg/m^3.

Rider and equipment mass
Trek reported via social media Jens' body weight to be 76kg. It may have been a little more but it's not a number that is particular critical to the calculations, as this is all about power and air drag.

Bike/kit mass - I'm going to assume ~ 8kg, again the calculations are not overly sensitive to this value.

As an example of this insensitivity, changing rider's mass by 5% only introduces a 0.3% error into the W/m^2 calculations.

Rolling resistance
I'm going to assume a coefficient of rolling resistance (Crr) of 0.0025, which is about typical for a quality set of track tyres on a quality wooden indoor velodrome. I did some calculations for Crr of 0.002 and 0.003, which is quite a broad range for such tracks and tyres and it only changes the power demand by approximately  +/- 1.5%. This is because rolling resistance accounts for less than 10% of the total energy demand for the event.

Power and coefficient of drag area
OK, so given all that, what power and aerodynamic numbers would be required to do what Jens did?

Well we can't really know what power Jens averaged for the effort unless Trek release the data, but what we can say is what his power to air drag ratio was. To ride that speed, it would be in the range of 1715 to 1750 W/m^2.

That's an average, as of course Jens' actual instantaneous CdA did vary as he changed position on the bike at times. He was mostly in his aero bars but was occasionally standing up on the pedals or making other adjustments.

This chart shows the line along which Jens likely falls somewhere. If his power was lower, then his CdA must have also been lower in order to maintain power to drag ratio in the range of ~ 1715-1750 W/m^2.

The chart also then shows what his power to body mass ratio would be (assuming 76kg), so we can see the wide range of power capability possible to attain such a speeds. You don't need big power, if you are very slippery through the air.

Aero matters. A lot.

Read More......

The Elusive Dopeometer

Readers of this blog no doubt have seen a number of examples I give about the (in)accuracy of estimating power from climbing speed, and in particular the confounding impact of wind on such estimates. Any climb with wind is going to be subject to error, and it doesn't take much wind at all to introduce quite a sizeable error.

There was my 2010 post about Alpe D'Huez ascent times, timely given the dual ascent this year, and my item yesterday about the significant error introduced by that great unknown, the wind.

I consider such W/kg estimates to be fine for a bit of pub chat fodder, but as a serious means to detect doping, really? I'll get back to this in a bit.

What has been more amusing than climb power estimates was more twitter/blogger/forum sphere musings on the power differential estimates from the Stage 11 individual time trial. Seriously. People are actually thinking they can reliably estimate the difference in power output of riders based solely on their time or speed in an individual time trial.

What complete and utter nonsense.

Aside from that affront to physics by Gazzetta dello Sport's Claudio Ghisalberti, there was also a post by the somewhat infamous Dr Ferrari about speed differentials from the same ITT and what that meant for power differences. Now Ferrari did say that this assumes all riders have the same "aerodynamic efficiency" as he calls it, which he then points out they don't.

So, given that they don't, why would you then proceed to produce and publish numbers as if they were all the same? More nonsense.

All this does is misinform the debate and feed Internet trolls.

OK, so people get the concept of comparing climbing performances (or attempting to) using power to body mass ratios, the now ubiquitous W/kg numbers. But can you do something similar with time trials over flatter terrain?

If you want to normalise flatter terrain ITT data, then you can make a reasonable stab at the differential of each rider's power to aerodynamic drag ratios i.e. the rider's time trial wattage output divided by the rider's coefficient of drag area (CdA), measured in units W/m^2. Of course this assumes the same wind conditions apply for the riders being compared which can be problematic in itself when the riders being compared are on course several hours apart (as was the case for instance with Tony Martin and Chris Froome).

On flatter ground, the higher your W/m^2, the faster you will go. This neat chart courtesy of Robert Chung shows the close relationship between flat road speed and power to aero drag ratio:

Hence we can reasonably say that the faster rider on the day has a higher W/m^2 (putting wind differences to one side of course). This is the flat land equivalent of the hill climber's W/kg.

What we can't say however is how much of that speed difference is due to higher power output and how much is due to a lower CdA. Indeed, it's possible for a rider to produce less power than another yet go faster if their aerodynamics is superior.

I’ve dealt with many riders of similar morphology who have significantly different CdA. I have a former team mate who was same height and weight as me (actually he was a bit heavier) and we have similar power output as well (mine was a bit better), yet his CdA is ~ 20% less than mine on our respective pursuit bikes. Our equipment was very similar. His natural body shape on the bike means he is just far more aerodynamically gifted. That’s why he medals at worlds and I don’t even make state finals.

Unless you know each individual rider’s CdA, attempting to derive power differentials from ITT speed is just pissing in the wind.

In this 2011 post I provided a short snapshot into this, with data provided by Andy Coggan who devised a draft variation to his Power Profiling tables, this time creating an Aero Profiling table:

The top of that list is a good indicator of what's required to set/break Boardman's hour record of 56.375 km (35.030 miles), now classified by the UCI as "best human effort".

Now if people think getting pro riders or their team management to release their power data is proving difficult, try getting their wind tunnel or aerodynamic field test data.

The Dopeometer

OK, so let's get back to obtaining riders' power meter data and using it as a dopeometer.

This seems to be a popular request. Greg Lemond wants the data released, as do the Bike Pure people. All over the net on forums and blogs and twitter and so on people are calling for the data to be released. The point being such transparency is a good thing, and I have no argument with that. But will it actually help? Or will it just be a public relations exercise and not really provide any additional insight into the issue?

Let us for a moment imagine that tomorrow morning we all wake up to find Froome and his professional riding colleagues and competitors release their power meter data.

Then what?

Will having more certainty over the accuracy of power data help us confirm or deny doping status?
A: No. All it will do is re-emphasise confirmation bias for those with an opinion one way or another.

What power output will confirm doping and what won't?
A: Nobody actually knows. All we have is differing opinions on the subject of what constitutes possibly suspicious performances. Yet people already have their suspicions. An SRM file isn't going to change that.

Just where is the doping power plausibility line? Can we really assign such a line? Is 6.2W/kg for an hour proof? 6.3? 6.4? 6.41?
A: In reality we simply can't put a clean line in the sand. The line for each rider may be different, and the line may vary depending on context. How long was the effort? When did it occur? What were the environmental conditions? How steep was the climb? Was it solo or with others? Was it a consistent effort or variable? Who responds better to doping?

Will it change which riders should be placed under scrutiny?
A: No, we already know who they are. They ride bikes professionally and at the elite level, win races and/or go up hills faster than the rest of us mere mortals.

Will it make doping detection easier?
A: Hardly, since proof of doping requires a positive test, a confession or reliable testimony and evidence, and we already know who should be scrutinised.

Will it prove riders aren't doping?
A: Of course not. Since it assumes there is an arbitrary upper power limit for doping to be confirmed, it does nothing to pick up any doping by riders who are below whatever that arbitrary limit is. No green jersey contender for instance is going to out ride the GC contenders on major cols. Hence such data only serves to tell us what we already know, i.e. a handful of riders finished ahead of their competition on the mountain top finishes.

Can power data be manipulated?
A: Yes, of course it can. Accidentally, inadvertently or deliberately. So then we'll have those on the conspiracy trail of a new doping detection avoidance technique of "data doping". Since we already know the amount of slop in power estimates from other methods, then fiddling with the numbers means no-one can really know if numbers are fiddled or not. There are of course forensic data analysis techniques that can identify some examples of that, but only if crude data manipulation methods are used. If riders and their support people are clever enough to manipulate blood to avoid detection, I'm pretty sure they'll be able to work out how to manipulate data to avoid detection.

Has "data doping" happened before? 
A: Sadly, yes as this example shows when a rider attempted to use doctored power data to prove a performance benefit from using a particular type of cycling equipment. Fortunately in this case the fraud was detected - but it took a Professor from Berkeley to point it out.

What would it cost to run such data collection in an independent manner, and free from possible manipulation?
A: Millions of dollars. Think about the number of bikes in the ProTour, the need to carefully calibrate say 1,000 SRMs, to have non-tamperable data loggers, to ensure all riders correctly perform zero-offset checks before and during races. The data collection process. Staff to manage this. Millions of dollars that perhaps would be better directed at improving doping control processes, technology, reducing testing costs, and simply performing more tests and more frequently testing in and out of competition.


I get that people want to see the data, and hope it's a short cut way to provide certainty around establishing whether a particular rider is doping. I get that release of such data may appear to increase transparency. But at the end of the day we'll just be back to where we started before all this data becomes available: i.e. none the wiser about riders' doping status.

SRM make a fine power meter, but it's not a dopeometer.

Read More......

Aero Profiling

Earlier this week I posted this item about power to aerodynamic drag ratio for the individual pursuit.

I mentioned in that item a table prepared some time back by Andy Coggan, which was similar to his power profiling table (which lists typical power to body mass of riders - W/kg for various time ), except it showed Functional Threshold Power (FTP) relative to aerodynamic drag (CdA) - W/m^2, instead of as per the original power profiling table.

The top end of the table would represent what's required to set a World Best Hour record.

In this way, a rider's power to aero drag ratio can be compared against the world's best.

Andy has kindly sent me the data, so here is the table for reference. Thanks Andy.

Enjoy!
(click on the pic to superaeronate)

Read More......

Individual Pursuit - What Makes us Faster?

A long time ago, in a galaxy far away, a Jedi Knight called Andy Coggan developed an insightful (but often misunderstood) table of numbers known as Power Profiling. Power junkie cyclists have been (mis)using the table to psych out their mates for years now.

The Power Profiling table lists power to body mass ratios for four key durations: 1-hour, 5-minutes, 1-minute and 5-seconds, chosen to reasonably represent the energy systems/physiology that predominantly underpin performance over these duration, i.e. (respectively): lactate threshold, maximal oxygen uptake (VO2max), anaerobic work capacity & neuromuscular power.

Power to body mass ratio is an excellent overall predictor of performance potential. It is especially good for determining performance when climbing hills.

However, performance in flatter time trials and individual pursuits is much more a function of power and aerodynamics than it is of power and body mass. Body mass of course impacts aerodynamics, however the relationship between them is variable, with overall morphology and position on a bike far more influential than body mass per se.

So, when choosing the one performance factor most important for flatter time trials and pursuits, one needs to focus on improving a different ratio – the Power to Aerodynamic Drag* ratio (power to CdA ratio - W/m^2).

The higher the W/m^2, the faster we go. Pretty simple really.

In 2009 Jedi Knight Coggan, being somewhat prescient, developed a draft version of his power profiling table, this time expressing performance in terms of the ratio of 1-hour power to CdA . I’d love to share a link to it, but I’m not sure I have a public location I can point you to (it was originally posted on a discussion forum about two years ago which has suckerific search function). I’m sure either Andy will provide a link, or post up a new blog item about it at some stage.

In any case, I thought at the time it might also be of interest to develop a similar table for the Individual Pursuit, so Andy whipped up one for me, and I then took that data and created a chart and table. Now that was nearly two years ago and I've been meaning to do a blog post about it ever since! Okay, so it's a little late but here it is.

The table show times for 2km, 3km and 4km individual pursuits and the corresponding W/m^2 required to attain that performance (click / right click to show full sized version):


So, for example, if you want to ride a 3km pursuit in 3:35, you will need a power to aero drag ratio of about 1900 W/m^2.

Alternatively, if you know your power and pursuit time (on a fast track), then you can back calculate an estimate of your CdA. e.g. a rider who completes a 4km pursuit in 4:30 requires a power to aero drag ratio of ~ 2200W/m^2.

If we know their power output we can then estimate their CdA. Let’s say they averaged 480W.
CdA = (480W) / (2200W/m^2) = ~ 0.218 m^2

It’s not perfect of course, just a guide and there are many factors to consider. Besides, if you have a power meter on your track bike, there are better ways to determine your CdA.

The chart below plots the same data, as well as show where on the chart the current world record holders appear for the following categories:

Elite Men & Women
Junior Men & Women
Masters Women

Hence, these world records represent the current upper limit of W/m^2 for each category:


The records are from the UCI website here: Track World Records

With the exception of Sarah Hammer’s WR in Aguascalientes, all of the others were set at sea level and in indoor velodromes (and so the assumptions used for the table data will be closer to the mark).

In the case of Sarah Hammer, due to the significantly reduced air density at altitude, it is probable her W/m^2 is overstated and is a little less than previous world record holder Sarah Ulmer whose record was set at sea level. The Power/CdA estimate for Ulmer’s 3:24.537 ride is 2200 W/m^2.

One thing the chart emphasises is just how much one needs to improve W/m^2 in order just to go even just a few seconds faster. When you are near your physiological performance (power) limit, we can see how important aerodynamics are to overall performance.

And just how freakin good those world record rides are.


Now of course there are some assumptions used to make up the data for the tables (assumption are shown on the table and chart). For example, it does assume a pretty fast track/tyres at a typical sea level air density, but really it’s just a guide, and serves to emphasise the importance of aerodynamics and thinking in terms of W/m^2 when working out what to focus on to improve your pursuit and time trial performance.

If your track and/or tyres are slower than the best, then it’s likely the performance suggested as attainable from a given power to aero drag ratio is overstated (or the W/m^2 required for a given performance is understated). Also, the rate of change in kinetic energy and associated variable power demands will also have some impact on these estimates. These data have used typical assumptions for that, but of course everyone’s initial acceleration, mass and fade in speed during their pursuit rides are different.

I’ll look into doing a similar chart for the hour record at some stage.

Where do you fall on the table?


For those interested in more discussion on factors impacting pursuit performance, then these items by Andy Coggan are a great place to start:

Demands of the individual pursuit, part 1
Demands of the individual pursuit, part 2



* Aerodynamic Drag is expressed as the combination of our two factors:

- Coefficient of Drag (Cd), a unit-less measure which is related to the shape of an object and how that affects air flow around it (e.g. think of a brick vs a bullet shape, the bullet shape has a lower Cd); and

- Effective Frontal Area (A), measured in square metres (m^2) which is how much area we present to the air (e.g . compare a van and a Mack truck – the truck has a larger frontal area and has to push more air).

These two factors are multiplied together to determine how "slippery" we are through the air.

Some example typical CdA values:
Commuter cyclist: 0.4 – 0.7 m^2
Road racing cyclist: 0.26 - 0.38 m^2
Time trial/pursuit rider: 0.2 – 0.3 m^2
Sports car: 0.5 - 0.6 m^2

Read More......

Another Hour of Power

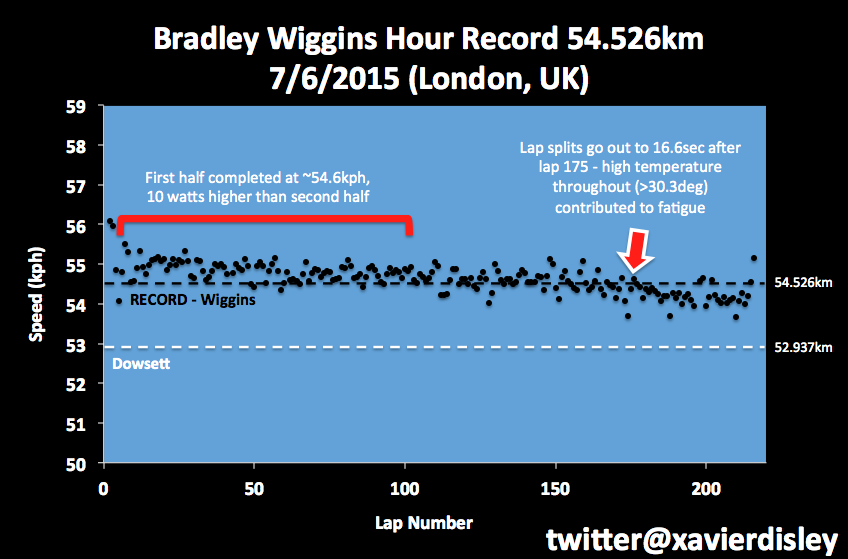
48.317 km.

That’s how far Jayson Austin was calculated to have ridden on his second and successful attempt to set a new world record for Masters Men (35-39) distance ridden in one hour. It added a huge 2.676km (5.8%) to the previous record set in 2007 by Jason Sprouse of the USA.

Jayson on his way to a new World Record

It is also the second furthest ridden by an Australian, with Brad McGee holding the honour of the furthest distance (not sure exactly how far but it is something over 50km).


It’s also about the same length as this post, so be warned!

I wrote about Jayson’s previous unsuccessful attempt in this post: An Hour of Power, which has been one of the more popular reads on this blog.

So what went right this time? How did Jayson add a whopping 3.649km (8.2%) to his previous attempt where he managed to ride 44.668km?

More excellent photos on the ride taken by Trevor Mullins can be found here:
http://tregan.com.au/photography/Sport/Cycling/One_Hour_Record/

As I have mentioned before, there are three things that primarily contribute to a fast time trial (or in the case of the hour record, to maximise distance ridden):

• Power to the pedals
• Piercing the wind (plus fast tyres)
• Pacing the course

I’ve previously explained these Three Ps in this post: Old Skool.

OK, well let’s consider his first attempt at the record last year.

Power - Feb 2008
Average Power: 241 watts (4.0 W/kg)
Normalised Power: 259 watts (NP:AP = 1.07)

Jayson took quite ill in the weeks leading up to the event and he was clearly not in the form he would have normally expected come race day. In hindsight he probably should have postponed. However that is a difficult choice as the logistics to organise the event make that tricky. In addition, on the day the timing system failed and Jayson had to abandon the attempt after 5-minutes and do a restart. That certainly did not help his cause at all. Jayson also chose to use a gear far too large for his form on the day.

Average Power for his first attempt was 241 watts. Normalised Power was 259 watts, giving a ratio of NP to AP of 1.07. For an hour record attempt, that is a very high ratio and one would expect a very well paced effort on a velodrome would see that ratio being very close to 1.00.

Piercing the wind - Feb 2008
Using the data available from the SRM power meter on Jayson’s bike, I concluded his CdA (a measure of how slippery you are through the air) was in the vicinity of 0.190m^2. That is very slippery for a bike rider by any standard. So Jayson had a pretty slick set up and position. Riding 44.7km with an average power of only 241 watts certainly indicates he was piercing the wind just fine.

Combined with his power, the ratio that most determines the speed a time trial rider will travel at is their sustainable power to aerodynamic drag - FTP : CdA - ratio.

In Feb 2007 that ratio was 241 / 0.190 = 1268 W/m^2

Pacing - Feb 2008
In essence, in the context of his sub-standard form come race day, Jayson simply paced poorly, making the classic mistake of going out too hard and fading. Badly. Ignoring the pacing signals from his coach, this was well and truly demonstrated by the charts in the first linked post, showing how much he faded through the course of the attempt, finally hitting a brick wall at around the 45-min mark.

Breaking his average power down into 15-min sections shows the dramatic fade in power:
00-15 min: 302 watts
15-30 min: 272 watts
30-45 min: 242 watts
45-60 min: 151 watts

I suspect what Jayson did was to ride at a level he felt he would be able sustain but that turned out not to be the case. C'est la vie.

Using my pacing analysis models (something I haven’t written about in any detail here), I have rated Jayson’s pacing with a Pacing Score of 0.960, which is, in fact, the lower anchor point on my relative pacing performance charts (i.e. indicating very poor pacing). A best in class Pacing Score is 0.995 (with 1.000 being theoretically perfect pacing).

To put that into context, if Jayson had ridden with best in class pacing, even with the reduced power at his disposal on that day, he could have added another 1.5-1.6km to his ride distance. He missed the record that day by 974 metres.

These are tough mistakes to make and hard lessons learned. But we often learn more from having the courage to make mistakes. Certainly both Jayson and his coach would have felt a little burned by the attempt (what some may not know is that Jayson had, in training, already beaten the record, just not officially sanctioned with UCI supervision, electronic timing, doping control etc etc that is required for an official record to be set).

In the months following, Jayson’s riding, form and morale slipped somewhat and his coach (a friend of mine), who was moving onto other projects, suggested Jayson speak with me about taking him on and getting him back on track. So Jayson and I discussed where he was at and set ourselves the objective of having another crack at the hour (as well as other racing objectives along the way).

For me, what was going to be important was that Jayson demonstrated a willingness to learn from the mistakes made (both from the ride specifically but also in general). You can be sure that these lessons were not lost on coach, and I consider them to be a substantial contributor to Jayson’s excellent performance the other week.

The biggest failure this time round would not have been missing the record, but in repeating the same mistakes.

OK, so how did the successful ride compare?

Power - Apr 2009
Average Power: 302 watts (5.0 W/kg).
Normalised Power: 303 watts (NP:AP = 1.00)

That’s 61 watts (+25%) more than his previous attempt. Now that’s gotta help. How did he manage it?

This time round Jayson did not get ill before the event. Nevertheless he is still relatively prone to illness, niggles and for some reason, a little accident prone as well (he even had a crash a few weeks before the attempt which did disrupt preparations a little). Jayson also works a full time job, with a lot of manual labour required (he works in the commercial flooring industry). So the ramp up of his training loads were pretty carefully managed to avoid increased susceptibility to illness and at times recognise that his work was sometimes tough on his body and training needed to be cut back. Even so, there were times when Jayson would do more than coach liked, and guess what? – the niggles would appear soon afterwards and training would be compromised.

Over time Jayson really started to appreciate the sense behind carefully managing the training loads. It enabled consistency of training and from that follows a steady and sustainable improvement in form. Jayson told me his form “sort of snuck up on me”.

Of course I did not confine Jayson to just training. Racing was a reasonably regular part of the diet. Every rider needs that little extra motivation at times, and pinning a number on your back is an excellent way to do this. As well, in the final weeks before the attempt, we minimised his exposure to Sydney’s busy roads, with a majority of rides being either with me, a trusted mate, at Centennial Park, on the velodrome or on my purpose built ergobike, Thunderbird 7.

Clearly Jayson has an engine and can really dig out some excellent power at times. What he lacked when we began working together, some 40 weeks before his hour ride, was depth of fitness. Despite very low training loads, he is way too capable of putting the hurt on and suffering the consequences. For those that understand the numbers, his chronic training load (CTL) at the time we started was ~38 TSS/day.

At the time of his hour ride:
CTL: 86 TSS/day
TSB: +10 TSS/day (training stress balance)
CTL/ATL Time Constants: 42/7 days

I did not have Jayson doing huge volumes. What I did do was ensure Jayson was doing quality work. Good solid endurance. Plenty of sweet spot / tempo work. Threshold tolerance work. And during the specific race preparation period, high end aerobic power work and specific threshold work on the track bike and in aero position at the track. The limited taper involved cutting back volume while using short but relatively intense intervals at the higher end of his aerobic power level abilities.

Here is a comparison of his power last time and this time:



Piercing the wind - Apr 2009
OK, so I have already established that Jayson was pretty darn slick through the air. But was any further improvement possible? Well yes as a matter of fact. Some positional changes, a different set of aero bars (based on a British Cycling design) and use of double disk wheels resulted in Jayson’s CdA lowering to around 0.185m^2. That’s a 2.6% improvement. It doesn’t sound a lot but that is worth approximately another 420 metres to his ride.

The bike exactly as ridden.
Thoroughly checked to ensure full compliance with all UCI regulations.
Note placement of the SRM PCV under the saddle.

Of note was that on this attempt, Jayson rode with a standard "under ball of foot" cleat position. In Feb 2008, Jayson used a mid-foot/arch cleat position. The fact that improved aerodynamics was achieveable despite the higher saddle position required of the regular cleat position would not be lost on some astute readers. Jayson also received a lot of support from fit guru Steve Hogg, mainly addressing many of the regular niggles, minor adjustments, use of various stem options, different saddles etc.

During training at the track, where possible, changes in position or equipment were compared to assess the differences. An alternative aero helmet was tried for instance and found to be substantially less aerodynamic than the Uvex that Jayson used. This is one of the direct and practical benefits of using power meters. It removes much of the guess work and objective decisions can be made based on the data.

So now Jason's FTP:CdA ratio is 302 / 0.185 = 1632 W/m^2

Even so, I would say that further improvement with his aerodynamics is still possible. There are still several minor details which, with enough solo track time, I would like to have tried and tested but they will just have to wait for another day.

Pacing - Apr 2009
Well I’m glad to report that Jayson now has the unique honour of topping the pacing league table, with a Pacing Score of 0.998, the best score I have ever recorded, as well as being the low anchor point (0.960).

Let’s just say that of the things that were drummed into Jayson’s head, pacing was what I was most concerned with. I knew he had the power. I knew he was slick. But would he be able to execute?

To ensure that happened, we did a lot of work in the weeks leading up to the attempt focussed on pacing. I developed a means to clearly communicate pacing information to him and Jayson began to develop an excellent “feel” for how to augment his effort ever so slightly each lap to maintain a sustainable pacing level. His choice of gearing was part of that strategy.

One thing went against the “conventional wisdom” – Jayson’s average cadence was 112 rpm. Conventional wisdom says Hour Records are all but set with a cadence of ~100rpm give or take 1 or 2 rpm. Bollocks to conventional wisdom I say.

Pacing information, lap times etc were conveyed on a regular basis

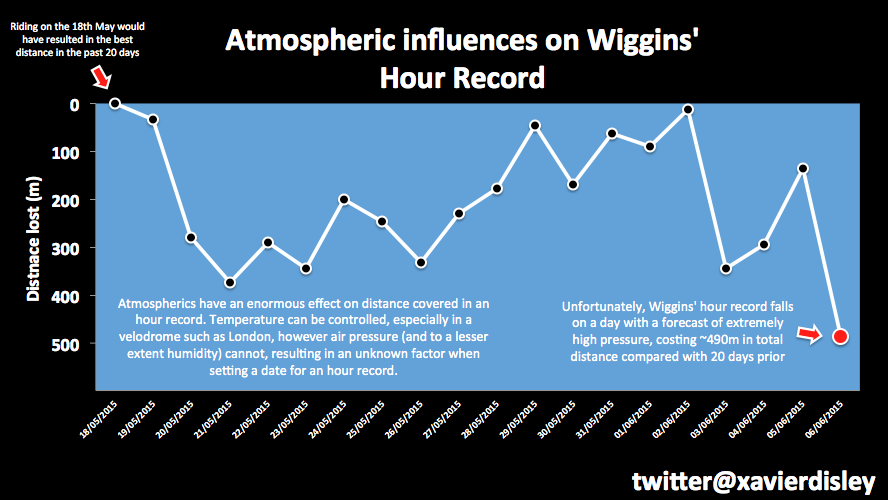
We also knew that different environmental conditions would impact on the sustainable pace on the day and we trained on different days with subtly different conditions. On the day of the attempt I checked both the air temperature and air pressure and that would tell me what pacing would likely be sustainable (and what wouldn’t). Dunc Gray Velodrome is not climate controlled and the temperature can and does vary quite a lot.

For example, a 5C drop in temperature would reduce the distance ridden by ~ 280 metres and an increase in air pressure of 20hPa would mean another 315 metres lost. Fortunately it was not a cold (21C) nor a high pressure (1004hPa) day although it had been warmer in training. Also, we requested that all windows and louvres be closed so as to minimise any potential wind disrutption and to retain as much heat inside as possible (April is Autumn in Sydney).

Of course the athlete is the one that must make a call on how hard to go but I had developed a very good understanding of his body language and could tell when it was too hard. Jayson was never going to go too easy, that’s for sure. My main concern was keeping a lid on it in the opening minutes. Jayson was made well aware of the lap times and how that played out relative to the existing record. The pacing mistakes were made in training, and ironed out in training.

On race day, nerves and adrenaline took a hold (I expected it, heck coach was nervous too!) and Jayson’s pacing was a little up and down in the opening minutes. However he made rapid adjustments knowing full well what over cooking it would do. It took quite a while but once he settled into a rhythm, his pacing was metronomic. Average lap times around the 250 metre track were 18.59 seconds (not counting the opening lap).

We had planned for a couple of “rest” breaks, where he could sit up, stretch, relieve any pressure points for a lap or so but as it turns out he didn’t need that and remained firmly in position for the entire hour. At times he varied his pace a little, and sometimes pushed himself back in the saddle, which was quite deliberate and helped him to stay comfortable and keep his concentration going.

Here is a comparison of his speed last time and this time:

That's more like it!

Thank you to:
Apart from Jays actually having the gumption to have another crack and delivering, there were many others involved in helping him get there and all should rightly share the success, including his former coach (hi Peter) who introduced him to training with power in the first place and showed what was possible, sponsors, the officials who helped coordinate the venue/UCI/ASADA etc, our club chief Mike, Jayson's family/support crew, Steve Hogg who was very accommodating with equipment and constant positional adjustments, training and racing buddies who kindly lent special gear (wheels, bars) for the attempt and rode/raced with Jays during the build up. And then all those that showed up to cheer him on!

Footnote:
Just six days after his record breaking ride, Jayson was knocked from his bike by a car while on a ride by a “hit and run” driver. Knocked unconscious and very, very nearly run over by another oncoming car, who’s driver managed to stop with the bumper bar over Jayson’s head, he is lucky to be alive. Jayson was admitted to Manly hospital and fortunately suffered no broken bones. However he did suffer from a sizeable haematoma and severe swelling of the thigh which required emergency surgery to open the leg (a fasciotomy) so that excess fluids could be drained and the swelling would not prevent blood flow. That was successful but now he has a large open wound which will take some weeks to heal.

He has since been discharged and it will be at least eight weeks before he can work or ride. As you can imagine Jayson is pretty pissed off about the incident but otherwise is in good spirits.

So now it will be onto the next challenge, getting an injured soul back to good form. That's something I have some experience with.

Well done Jayson! A super ride.

Photos: David Lane, Action Snaps:
http://www.actionsnaps.com.au/

Read More......