Warning. Bike geek talk follows involving maths and physics, although I'll spare you the calculations and just provide the charts summarising the outcomes.
In this February 2013 post "The sum of the parts", I discussed the relative importance of wheel mass and wheel aerodynamics during accelerations using a technique known as forward integration, and based on the mathematical model of road cycling power by Martin et al.
As I said back then, aero and weight are not the only wheel performance factors to consider, but these are the two I am going to examine here, since they are the two factors most often conflated with respect to their relative importance. Read my earlier post for a long list of other factors to consider.
In that item I made some assumptions about the scenarios being compared and said I would return one day with an updated version using better assumptions applied to the forward integration model.
I’ve now had the chance to do the revised modelling, and I was prompted by some recent forum postings once again promulgating the wheel rotating mass is really important myth, since it’s an often misunderstood concept.
So I’m going to run some numbers through the model for three scenarios:
- A standing start acceleration lasting 10-seconds on flat windless road,
- A rolling start acceleration lasting 10-seconds from an initial speed of 30km/h
- A rolling start acceleration lasting 10-seconds from an initial speed of 15km/h and heading up a 4% gradient
For the first I will examine the impact of adding mass to the wheel rims, and then for each when adding that extra rim mass comes with an aerodynamic benefit.
This time I have added extra features to the model to improve its realism. These are:
i. Including calculation of the rotational kinetic energy of the wheel in the model. Previously I had simply overstated the wheel mass difference as a (not unreasonable) means to compensate for not including a calculation of changes in rotational kinetic energy.
ii. Using a power curve in each scenario that is more realistic. In the original model I used a flat 1000W power curve, but of course no one generates power in such a manner. So this time I used power curves for a standing start and a rolling acceleration based on sample accelerations from my own (post amputation) data.
Rotational Kinetic Energy demand of accelerating wheels is small
The amount of additional energy or power required to accelerate a heavier rim at the same rate is very small, but nonetheless, I added it to the model for the sake of completeness. In this revised model I only considered the case of adding extra mass at the rim, since this is the “worst case scenario” for adding wheel mass, and happens to also be easier to calculate the moment of inertia.
If you want to really examine the difference between two wheelsets, you'd need to know the moment of inertia of each wheel, but it will always be less than if all the extra mass is added at the rim.
So just how much is the difference in energy demand from adding extra mass at the rim?
Well if you consider a 5-second long acceleration of an 80kg road bike + rider on a flat windless road from 30km/h to 40km/h, it requires a 5-second average power of over 700W. Adding 250 grams to the wheel's rims will require a whopping extra 2.7 watts to attain the same rate of acceleration, of which half is the additional power required for the translational (linear) acceleration component, and half for the wheel's rotational acceleration component.
Like I said, the extra energy demand to accelerate additional rim mass is not much. But every little bit counts. Sum of the parts.
Standing Starts
So let’s begin with the standing start scenario (i.e. an acceleration from 0 km/h).
How much does adding 250g to the rim affect acceleration?
Well here are the model assumptions comparing each set up:
Below is shown the respective speed curves if we apply a standing start power curve typical for me, i.e. power rises quickly to a little over 1000W after 2.5-seconds, holds near that level for about 5-seconds, and begins dropping away after ~8-seconds as neuromuscular fatigue sets in. For reference, the 10-second average power as shown is 924W. You can click on the image to see a larger version.
The difference in speed curves for each scenario is almost impossible to discern - there are actually two speed curves but they overlap very closely, hence appear as only one.
So in order to assess the differences, I plot the difference in cumulative distance travelled at each moment in time. In other words, this chart plots how far ahead or behind the second set up (heavier rim) is after X seconds.
We can see the addition of extra mass at the rim reduces the acceleration slightly and after 10-seconds there’s a loss of 22cm compared with using the lighter rim. Cool, let's all rush out to get lighter wheels. Well, just hang on a minute...
Heavier but with better aerodynamics
As mentioned in my previous post, I’ve already shown a drop in CdA of 0.023m^2 in low yaw conditions between using a set of low profile spoked wheels, and a deep section aerodynamic wheelset. But you don’t need to believe me, there is plenty of wheel test data in the public domain, for example the one done many years back by Roues Artisanales showing the power absorbed for various wheels. For good aero wheels, the advantage increases significantly in cross winds. There are many other wheel aero tests available, and Jack Mott of Aeroweenie has put together a neat list of such datasets.
So what happens if that extra 250 grams of rim mass comes with an aerodynamic bonus reducing CdA by 0.023m^2?
Since the plot of speeds still shows very little discernible difference, and I’m applying the same power curve, I’ll go straight to the cumulative distance difference chart:
Initially the lighter wheel takes an advantage and gradually pulls ahead of its heavier but more aerodynamic rival, gaining a maximum advantage of 5cm after 5-seconds. However, as the acceleration progresses, the bike/rider with the heavier but more aero wheel begins to catch up, draws level and passes the light wheel rider after 8-seconds and finishes the 10-second effort with an advantage of 11cm.
So, not a lot in it, but remember that this is a standing start scenario, which is the quickest acceleration scenario there is on a bike, and where the impact of wheel rim mass has the greatest (albeit minimal) impact on performance.
In my previous post using simpler model assumptions I said that the lighter but less aero wheel set was good for a standing sprint of up to six seconds. Well with a power curve that’s a little more realistic (for me), that advantage extends to all of eight seconds. Beyond then and it won’t matter, the bike/rider with the heavier but more aero wheel will pull away. And the greater your standing power curve, the earlier the advantage tips to the aero wheel.
Rolling accelerations
OK, so what about accelerations from a rolling start? Well you should be able to guess the outcome of this one before reading on.
Here are the power and speed curves for a rolling start sprint effort.
In this case you’ll note that the peak power is higher than for the standing start, closer to 1250W occuring again after about 2.5 seconds (and incidentally sees me add about 1000W above the baseline effort of ~250W), but thereafter drops away consistently. This sort of power curve is normal for me from a rolling start as I can get pedal speed higher and more rapidly but I also experience a quicker decline from that peak than in the standing start. 10-second average power in this scenario is 989W (about 65W higher than the standing start).
Here’s is the cumulative distance difference:
The bike/rider with the heavier but more aero wheel pulls ahead as soon as they start their sprint and never looks back, ending up with a 58cm advantage after 10 seconds, or nearly a full wheel ahead.
Now of course the assumption with these comparisons is that all other properties of the wheels are the same, even so my original conclusion stands, even in races with hard accelerations.
The model can be run with anyone’s individual power curve, mass, CdA and Crr assumptions, as well as considering other factors such as gradient and wind.
Hotdog crit anyone? Sprint up a hill?
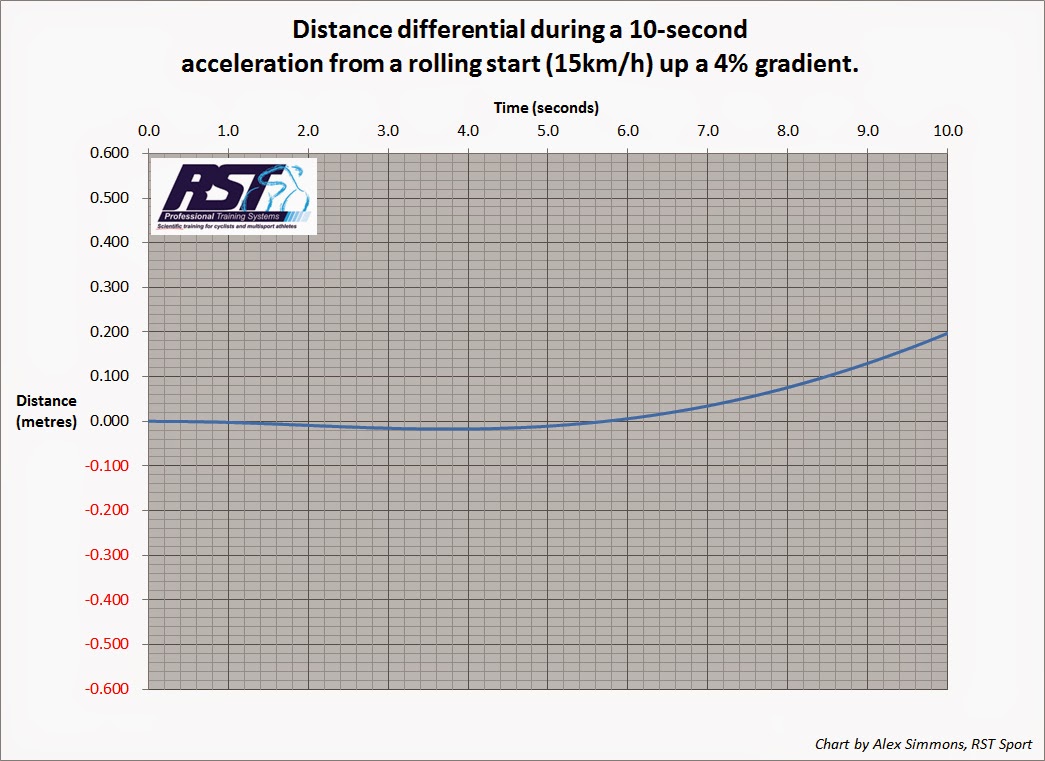
Let’s say we have the same bike, rider and wheel sets as above but this time the acceleration begins from only 15km/h and goes up a 4% gradient. Nasty.
Here the lighter wheel gains a maximum advantage of just under 2cm after 3.8 seconds, thereafter the heavier aero rim catches back up after 5.7 seconds and ends the 10 seconds sprint 20cm ahead.
If the finish line were 90-100m or more from the turn, I sure know which wheel I’d prefer to be using. If it was only 45 metres though, well it’d sure be a tight race and you'd need a high speed finish line camera to pick the winner!
Keep it steady son!
OK so the point of all this was to demonstrate the relative unimportance of wheel rim mass and why aerodynamics matters even when accelerating, as dynamic scenarios are somewhat harder to calculate than steady state cycling scenarios such as time trialling, or hill climbing where accelerations are very small and changes in rotational kinetic energy are zero, or so tiny as to be completely negligible.
For steady state cycling, well the heavier but more aero wheel still wins in just about every scenario.
For the rider in this set of examples, at 300W the bike/rider with the heavier but more aero wheel still climbs faster on gradients of up to 8%, and of course will descend more quickly as well. At 9% gradient it's line ball and once you go steeper than that, well the lighter rim is quicker.












16 comments:
Damn your good Alex! Thanks for working through all of this. Steve
Now that was interesting, very interesting. Thank you for all the work you put into it.
Alex, most everyone can relate to a 250g wheel weight difference - essentially the difference between the stock wheel you get when you buy your bike and the one you upgrade to. Can you give us a couple of examples of wheels at the two ends of the spectrum that would describe your 0.023m^2 drag difference?
Most good low profile pre-built wheels today are 21-23mm wide at brake track, 24-30mm deep, with 16 to 20 spokes on the front, and 21-24 on the back wheel. Popular low profile wheels like the Campy Zonda, Fulcrum Racing 3, Mavic Ksyrium SLS, Shimano C24 would fall in this category and weigh in the 1500g +/- 75g range.
What wheel dimensions or examples would you put in the deeper section/more aero profile range that would create the 0.023m^2 drag difference your are talking about? Would these be 45mm deep, 24mm or wider aero wheels like the Zipp 303 or Enve 3.4 or are we talking 60mm TT or even 90mm deep track wheels? Thanks
Great article !!! very useful information, I was always wondering about this myself
Accelerations don't exist in a vacuum. You've got to do the whole rest of the ride. This is dumb and most surely cannot account for the full reality of everything factor involved.
Why not do some real world tests instead of "models"?
@Steve
That's the sort of difference I measured between a pair of 32 spoke Velocity Aerohead rims, and deep section wheels such as the old Campag Shamal or an older model Zipp 808. Low yaw differences. Wheels like Ksyriums are even worse aerodynamically but good solid training wheels.
@Anonymous - lol, that's such a helpful observation. If you had read the post, and the earlier one linked, you would have seen a link to an article by Kraig Willett which extended the assessment over three real world examples of road rides.
But if this is so wrong, and you need real world examples, then ask yourself why elite track team sprint lead riders still use the most aerodynamic wheels over lighter options?
A: It's because they both accelerate more quickly and help attain a higher top speed than using a lighter but less aero option.
But is it really the aero factor, or is it the heaviness that makes it faster? Perhaps it is just the flywheel effect.
Calculate that. But that is still contrary to my own real world experience, and probably most others, or they wouldn't make wheels the way they do.
I think you're deluding yourself if you think can calculate this with a model.
When I rode 202 tubulars vs 404 tubulars on a 3 minute undulating twisty, turny, punchy, section, I broke my Strava pr by 3.5+ mph, from 22.9 to 26.4 on a segment that I have ridden 53 times.
Good luck pontificating from the lab though.
Improving your time by 3.5mph was obviously not due to going from 404s to 202s.... The difference between the two wheelset would never amount to that much. The problem with your so called real world comporison a is that you are not accounting for things like wind (huge impact) or even more basic... Can you say that you produced the same power on both rides? If on one attemp you had two water bottles full of water and the other they were empty that can mean 1 lb difference... Was it the same season or even month? Rider weight or even what you are carrying in your pockets can make a difference. That's why we call those annedoctes not evidences. Learn the difference
Anonymous - I'm happy to explain, but you have to be willing to listen and learn. Given your use of the phrase "flywheel effect" suggests you don't really understand the physics. As for being in a lab, hardly. lol
Alex, I recognize that you picked your 250g and 0.023m2 differences to demonstrate your point. In reality, few people are going to find themselves choosing between wheels as different as a low profile 32 spoke Velocity Aerohead and a Zipp 808. People typically are trying to choose between two pair of mid-depth race wheels or two pair of aero TT/Tri race wheels or two pair of lower profile all-arounds with lesser rim weight and aero differences. Other scenario would be riders weighing the value of upgrading from their heavy, not aero, low profile stock wheels to better low profile alloy wheelsets like those I mentioned or to a mid-depth, aero carbon wheelset.
Also, the amount of difference either in either of the extremes of dropping 250g of rim weight or between the lighter and more aero wheel is small (<1 meter) and perhaps insignificant on the road or track considering the effect of body position and any number of other factors that might be more significant. Are we to conclude that dropping that amount of rim weight or improving aero that much even maters in isolation, relative to each other or relative to other factors? Perhaps you could estimate how many times one makes those 10 second accelerations in a 40K (50 times?) crit or 100K triathlon (??) or other situations and add it up to put a total distance or time on it to further translate your model to a real world situation.
Thanks,
Steve
Steve, yes the post and models were meant to be illustrative and demonstrate just how small a factor wheel mass is, even for accelerations. The fact that the differences are small even when performing the hardest of accelerations is a key point.
When your choices are between two wheel sets that are very similar, then I suggest ignoring the mass difference and focus on aero and all the other wheel choice factors I go through in Part I of this item. Which factors you place higher priority on is often a matter of personal choice (e.g. cost, appearance), while I was assessing two choice factors which can be assessed quantitatively rather than subjectively.
As for other performance factors (e.g. body position etc) being larger considerations, yes of course, but one's body position doesn't change just because you are using different wheels. That's a separate issue, and this was a comparison "ceteris paribus".
Remember this was modelling *hard* accelerations, the one situation where wheel mass matters more (but as we have seen, still not that much). Aero matters *all* the time.
As for modelling races, well that's for another day.
For a triathlon or non technical time trial, accelerations are very small, and wheel mass matters little. Focus on your power/CdA ratio.
In a criterium, how many and how hard accelerations are is very dependent on the nature of a course (and partly how it is raced). A circuit with fast turns is very different to hot dog circuit with a U-turns every 400-800 metres.
Hi Alex,
Have you considered the effect of wheel weight on precession? Am I right in thinking your models assume no side to side movement of the rider/bike?
I always thought that might be what people 'feel' when they say they can feel the difference between light and heavy wheels. And if you have to put more energy into rocking the bike backwards and forwards, then you have less energy left to make it go forwards.
Does that make sense? I can expand if not.
Cheers
Great article. Have you tried a sinusoid all power model that takes into account the variation in power during each pedal stroke? Seems like there would be slight acceleration/deceleration on each stroke at high speed. What is the effect of wheel weight in that case?
Hi Joel
yes, see my later items where I do just that for both steady state cycling:
http://alex-cycle.blogspot.com.au/2015/01/the-sin-of-crank-velocity.html
and for acceleration scenarios:
http://alex-cycle.blogspot.com.au/2015/01/accelerating-sins-crank-velocity.html
Once you read those, you'll see the velocity oscillations are small, and changes in wheel mass would have a negligible impact on an already small effect.
Enjoy!
Alex
Thanks for this.
One thing I'm stuck with.... You can clearly feel some difference when going from a 2000g to 1500g wheelset. It's there, there's a feeling, everyone will feel it. You're left wondering what it is. Stuck in my head are the following factors:
1) This discussion usually happens in the context of watts, which is a power (force over time) measurement. The rider FEELS torque (force only).
2) The context when most people feel wheel weight is initial acceleration (accelerating at high gs).
3) Most people do initial acceleration in a too high of a gear. They just apply their body weight to get from 0-5mph. There is a leverage / resistance that is felt.
Anywho, If you start out in 50x21 w/ 170mm crank arm, you'll have a gain ratio of 4.7 (for every 1cm of pedal movement you'll have 4.7cm of wheel movement. Your 80kg of body weight torque is being turned into (80kg / 4.7) 17kg of torque at the wheels (100% efficiency here). Here a 500g of extra resistance is being felt as 2400g of extra resistance at the pedal. This is 3%, but it goes somewhere in explaining the tactile difference in wheel weight.
Acceleration Gs, I don't understand this math,but it may come into play :-)
Post a Comment