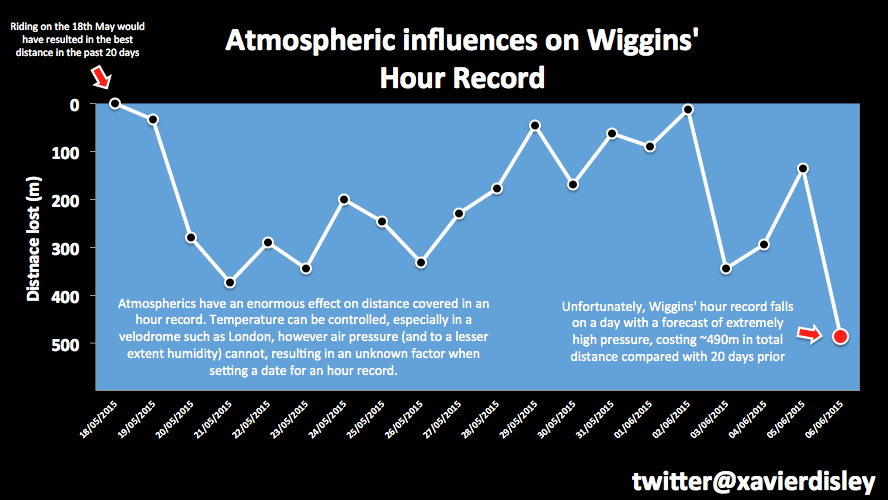
My colleague Xavier Disley did up a neat chart showing the impact the daily variability of barometric pressure can have on the distance attainable for an hour record, and how it's looking given the weather forecast when Xav last did the chart:
Nice - it shows how much breaking a record can still come down to a bit of luck with weather.
I think in Wiggins' case, assuming no major execution (i.e. totally crummy pacing) or mechanical issues, he'll break Dowsett's current mark no matter the weather as his power to drag ratio is sufficiently higher than Dowsett to overcome a slow air day.
But to set an outstanding mark such as Rominger's record, he'll need luck on his side. High pressure days are not good for speed.
Below is another version of this relationship between barometric pressure and distance attainable for four combinations of power and aerodynamic drag (CdA) values.
The chart is pretty self explanatory. For each combination of power and CdA chosen, the distance attainable reduces as barometric pressure increases.
That's because higher air pressure means a higher density of air molecules, and more air molecules to push out of the way requires more power.
A 60hPa difference in barometric pressure is equivalent to about 1km difference in distance attainable for the hour for the same power and CdA. That's a wide range of barometric pressure though, and variations are not normally quite that wide in most locations.
But a variation of half that is certainly possible over just a few days of varying weather as can be seen in Xavier's chart above.
I chose two power outputs: 430W and 450W, and two CdA values: 0.20m^2 and 0.19m^2. I don't know what Wiggins' power nor CdA value actually is or will be on the day, but for the sort of speeds he's likely to attain, these are in the ballpark.
It's the ratio of power (W) to aero drag coefficient CdA (m^2) that primarily determines the speed or distance attainable. hence why we refer to power/CdA ratio as measured by W/m^2. This chart covers a power to drag ratio range of 2150-2370 W/m^2.




2 comments:
Ouch. It's almost unfortunate this isn't a low-key attempt where it's a matter of extending some hotel stays to wait for a good day. This is his chance for history. It would be unfortunate for daily air pressure fluctuations to diminish his result.
Gerard Vroomen tweeted that because wind drag was "quadratic" to speed but only linear on pressure, it was a small effect. In reality the relevant issue is power, where it's the third power. But he's perhaps confusing high-order on the aggregate with high-order on the margin. For example, if I do a Taylor expansion on speed about a given average speed, quadratic effects may be very small. But quadratic effects on total speed are still 1st order, and we're still talking 550 meters is "only" 1%. But that's still huge.
BTW based on your previous post:
http://alex-cycle.blogspot.com/2014/12/wm2-altitude-and-hour-record-part-ii.html
It looks like there's maybe 1 part gain per 3 parts loss associated with altitude loss (pressure gain) for non-acclimated athletes at sea level, so for every 480 meters slower per your chart here, he'd actually be only 320 meters slower (due to 480/3 = 160 meters "gained" from higher power). That's just eyeballing the chart, though.
Post a Comment